Momento polar de inercia

La inercia es la resistencia que opone la materia al modificar su estado de reposo o movimiento. Esta propiedad se describe claramente en la Primera Ley de Newton, que postula:

"Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él."

El momento polar de inercia es la medida de la capacidad de un cuerpo para resistir la torsión alrededor de un determinado eje cuando se le aplica un par de fuerzas.

La torsión es un concepto ampliamente utilizado en mecánica, generalmente expresa el desplazamiento angular de un cuerpo sujeto a un par de fuerzas. Cuanto mayor sea el momento polar de inercia, menor desplazamiento sufrirá.

Este concepto tiene mucha importancia en el diseño del automóvil porque definirá su comportamiento en curva. Durante toda la curva, el coche trata de cambiar de dirección alrededor de su eje de gravedad, y cuanto más lejos del centro de gravedad se encuentren los polos de inercia, mayor será el momento de inerica y por ello su resistencia a describir la curva.

De forma simplificada, supongamos que tenemos una hoja de papel, sobre la que colocamos dos pesos (dos polos de inercia) y queremos hacerla girar sobre un eje determinado, como muestro en la figura.

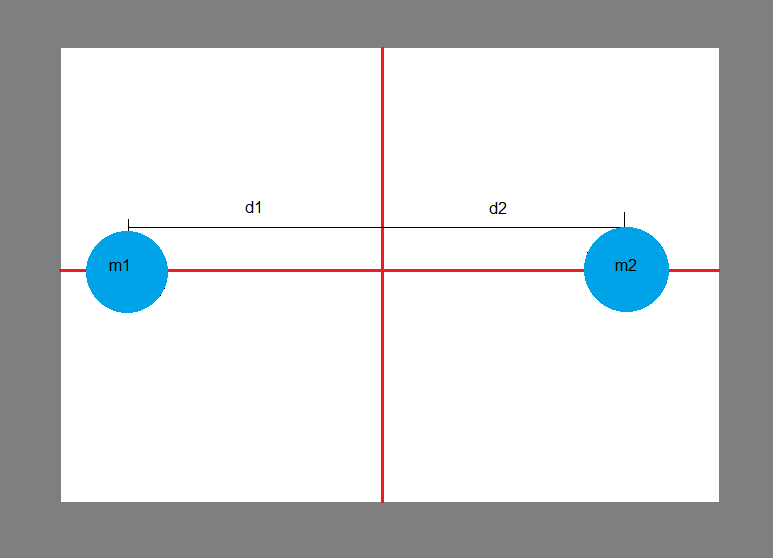
Cuanto más lejos del eje de giro estén las masas (m1 y m2 en la figura), más complicado será hacerlas cambiar de dirección.

En automoción definiremos el momento polar de inercia de un vehículo como la suma de los momentos polares de inercia de cada uno de los polos que vayamos a considerar:

ΣM = m1*d1² + … + mn*dn²

De la formula podemos extraer que grandes masas alejadas del centro de gravedad darán como resultado un alto momento polar de inercia, mientras que si las masas son menores o están más cerca del centro de gravedad tendrán como resultado un bajo momento polar de inerica.

Veamoslo ahora aplicado de forma simplificada al los casos prácticos de dos coches con diseños completamente diferentes. Consideraremos únicamente como polos de inercia el motor y la caja de cambios, ya que son los elementos que mayor influencia tienen en un vehículo. En un cálculo real se tendrán en cuenta todos los elementos del coche.

Las distancias se calculan desde el centro de gravedad del vehículo, al centro de gravedad de cada uno de los elementos.

Supongamos que el motor del Porsche 904 del ejemplo tiene una masa de 100kg y su caja de cambios 50kg. Supongamos también que el centro de gravedad del motor está a 0.4m de distancia del centro de gravedad del coche, y que el de la caja de cambios está a 0.8m.

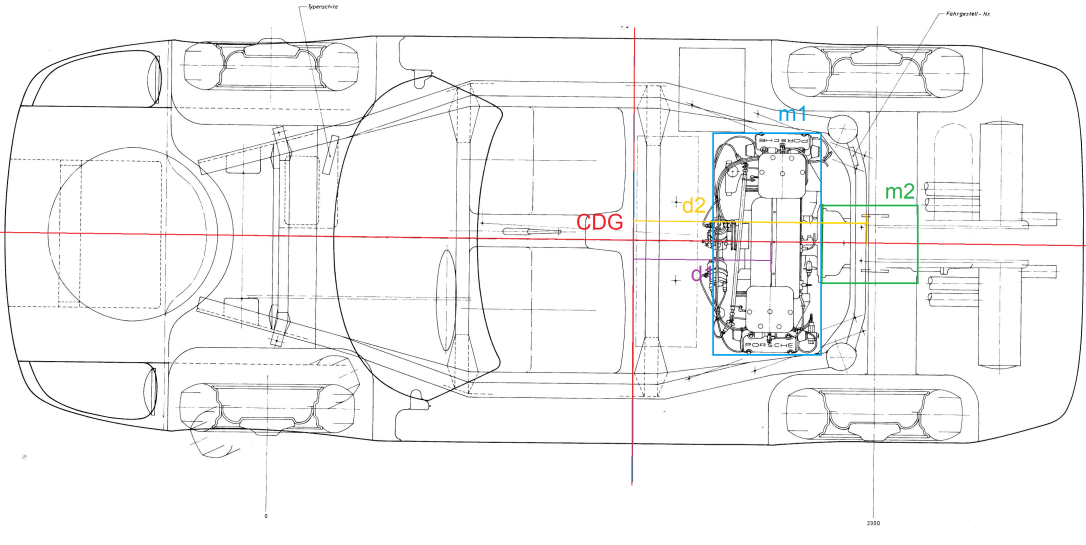
El resultado del cálculo para el Porsche 904 será:

ΣM = m1*d1² + … + mn*dn² = 100kg *(0’4m)²+50kg*(0’8m)²= 48kgm²

Veamos ahora los valores que devuelve el mismo cálculo para un coche con las masas muy lejos del centro de gravedad, como puede ser un Audi con el motor por delante del eje delantero.

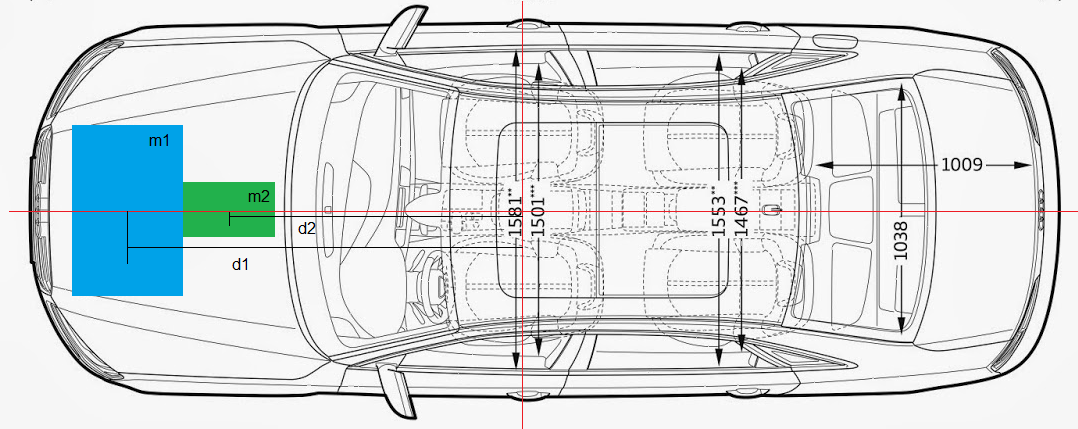
Supongamos que los valores aproximados son 100kg para la masa del motor (la real sería más cercana o superior a 200kg), 50kg para la caja de cambios; el cdg del motor está a una distancia de 1.5m del centro de gravedad y el cdg de la caja de cambios a 0.8m.

ΣM = m1*d1² + … + mn*dn² = 200kg *(1’5m)²+50kg*(0’8m)²= 482kgm²

Tras realizar el cálculo vemos que el momento polar de inercia es 10 veces superior en este caso, debido únicamente a la posición del motor, pues el resto de valores son idénticos en los dos ejemplos.

Esto implica que necesitaremos realizar 10 veces más fuerza para conseguir desplazar el motor y caja de cambios en el Audi que en el Porsche. Y toda esa fuerza tiene que ser ejercida por los neumáticos.

Por esta razón la gran mayoría de coches de competición tienen motor central y tratan de que todas las masas estén lo más cerca posible del centro de gravedad, consiguiendo un vehículo muy ágil, sin embargo también tiene como consecuencia unas reacciones mucho más bruscas.

Las posiciones de los polos de inercia influyen de forma decisiva no sólo en la agilidad del coche al tomar la curva, si no también al tipo de reacciones que tendrá. Un coche será netamente subvirador si sus masas están mayoritariamente en la parte delantera y será sobrevirador en el caso contrario.